Rational numbers are a pillar of logic and order, offering a comprehensive framework for representing quantities that can be expressed as fractions of integers.
Yet, the term “rational” might seem enigmatic at first glance.
G.O.D. is Rational
\(\frac{G}{D}\)
What is a Rational Number?
A rational number is any number that can be expressed as the fraction of two integers, where the denominator is not zero.
Rational numbers include integers […-1, 0, 1…] and fractions.
Examples of rational numbers include:
3 = \(\frac{3}{1}\)
\(\frac{1}{2}\)
\(\frac{3}{7}\)
\(\frac{-8}{9}\)
Decimals with a pattern that repeats can be expressed as fractions and as such are rational:
.3333… = \(\frac{1}{3}\)
Conversely, numbers that cannot be expressed as fractions of integers are called irrational numbers. Familiar examples of irrational numbers include the square root of \(\sqrt{2}\), pi (π), and the golden ratio (phiϕ).
This also includes decimals without a repeating pattern such as \(\sqrt{3}\) = 1.732050807568877293527446341505872366…..
The Rationale Behind “Rational”
The term “rational” finds its roots in the Latin word “rationalis,” which means “having reason” or “relating to reason.” The choice of this term to describe these numbers is not arbitrary but rather deeply rooted in the logical structure of mathematics. In natural language, people seldom mean the mathematical reason when using the word “rational.” However, on GodCandleMarket.com and throughout the Image Nation of Numeria the word “rational” may used interchangeably.
G.O.D. is Rational
\(\frac{G}{D}\)
Here’s the rationale:
- Expressibility as Fractions: Rational numbers are called so because they can be expressed as ratios or fractions of integers. This property aligns with the idea of reason and logic, as the relationship between the numerator and denominator in a fraction follows a clear and understandable pattern.
- Logical Consistency: Rational numbers adhere to the principles of arithmetic and algebra, making them amenable to mathematical operations such as addition, subtraction, multiplication, and division. Their predictable behavior under mathematical operations reflects the rationality inherent in their definition.
- Foundation of Number Theory: Rational numbers serve as foundational elements in number theory, which explores the properties and relationships of integers and their extensions. Understanding rational numbers provides a solid basis for studying more advanced mathematical concepts and structures.
4. Rates of Change: In action, rational numbers can also indicate rates of change. Such as \(Power= \frac{energy}{time}\)
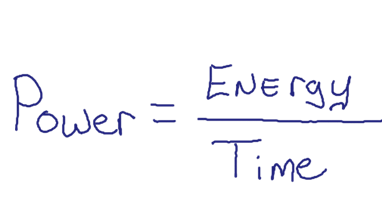
In essence, rational numbers embody the principles of reason and logic within the domain of mathematics. Their designation as “rational” stems from their expressibility as fractions of integers and their adherence to the fundamental rules of arithmetic.
By grasping the concept of rational numbers, learners gain insight into the systematic organization of numerical quantities and the logical underpinnings of mathematical reasoning.
