Sierpinski’s Triangle, a fractal named after the Polish mathematician Wacław Sierpiński.

To create Sierpinski’s Triangle, we follow a simple iterative (repetative) process. Start with an equilateral triangle and divide it into four smaller equilateral triangles. Remove the central triangle, leaving three smaller triangles. Repeat this process for each remaining triangle. Above we see the first 5 iterations of a Sierpinski’s Triangle.

Fractals, such as Sierpinski’s Triangle, provide a glimpse into the mesmerizing world of fractal geometry. These self-replicating patterns offer a unique perspective on the nature of infinity, recursion, and symmetry. By exploring the depths of fractal geometry, we gain a greater appreciation for the underlying structures that govern our mathematical universe.

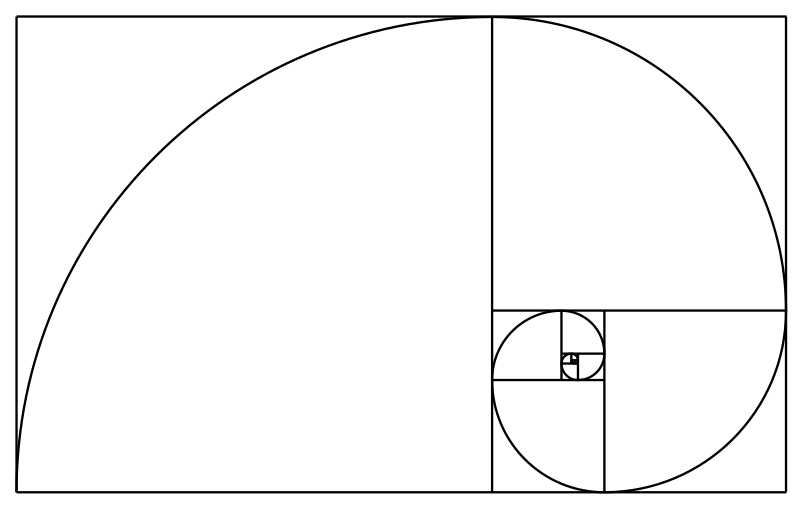
Its connection to the golden ratio adds an extra layer of intrigue, showcasing the harmonious relationship between mathematics and aesthetics.

By unraveling the mysteries of Sierpinski’s Triangle, we unlock a world of infinite complexity and beauty, inviting us to explore the boundless depths of mathematical possibility.

In the Image Nation of Numeria, we use the symbology of Sierpinski’s Triangle to represent the levels of understanding abstract material.